写写 SAM 这抽象玩意。
SAM(Suffix Automaton),后缀自动机,是用来解决有关字符串子串问题的一种数据结构。
我们知道,一个字符串的所有子串,其实也就是所有前缀的后缀。因此我们就诞生了一个想法:把所有后缀都扔到 trie 树上,这样我们就可以直接沿着字符走,并且能够获得所有子串的信息。
但是这样的空间复杂度是能够达到 O ( n 2 ) O(n^2) O ( n 2 )
在我们考虑这个问题之前,我们先来看另外一种东西,这个东西就是我们压缩自动机状态的关键。
为了方便叙述,我们定义整个字符串为 t t t
我们定义 E n d p o s ( s ) \mathrm{Endpos}(s) E n d p o s ( s ) s s s t t t t = abcaabcc t=\texttt{abcaabcc} t = abcaabcc E n d p o s ( abc ) = { 3 , 7 } \mathrm{Endpos}(\texttt{abc})=\{3, 7 \} E n d p o s ( abc ) = { 3 , 7 } E n d p o s \mathrm{Endpos} E n d p o s
而关于 E n d p o s \mathrm{Endpos} E n d p o s
当 E n d p o s ( a ) = E n d p o s ( b ) , ∣ a ∣ < ∣ b ∣ \mathrm{Endpos}(a)=\mathrm{Endpos}(b), |a|<|b| E n d p o s ( a ) = E n d p o s ( b ) , ∣ a ∣ < ∣ b ∣ t t t a a a b b b
两个字符串 a , b a, b a , b ∣ a ∣ < ∣ b ∣ |a|<|b| ∣ a ∣ < ∣ b ∣ E n d p o s ( a ) ∪ E n d p o s ( b ) = ∅ \mathrm{Endpos}(a) \cup \mathrm{Endpos}(b) = \varnothing E n d p o s ( a ) ∪ E n d p o s ( b ) = ∅ E n d p o s ( b ) ⊆ E n d p o s ( a ) \mathrm{Endpos}(b) \subseteq \mathrm{Endpos}(a) E n d p o s ( b ) ⊆ E n d p o s ( a )
对于同一 E n d p o s \mathrm{Endpos} E n d p o s [ x , y ] [x, y] [ x , y ]
我们根据这几条性质,我们可以想到树形结构。具体地说,一个等价类可以看作一个点,而等价类的包含关系则对应着树上的父子关系。这样我们就能建立一棵树,而每个点对应的父亲也就是我们在 SAM 中见到的 l i n k \mathrm{link} l i n k
更具体的定义 l i n k ( u ) \mathrm{link(u)} l i n k ( u ) u u u u u u
这里是 OIwiki 的定义
考虑 SAM 中某个不是 t 0 t_0 t 0 v v v v v v e n d p o s \mathrm{endpos} e n d p o s w w w w w w
我们还知道字符串 w w w t t t v v v t t t
换句话说,一个 后缀链接 l i n k ( v ) \mathrm{link(v)} l i n k ( v ) w w w e n d p o s \mathrm{endpos} e n d p o s
我们再设一个初始状态 t 0 t_0 t 0 E n d p o s = { − 1 , 0 , ⋯ ∣ t ∣ − 1 } \mathrm{Endpos}=\{-1, 0, \cdots |t|-1 \} E n d p o s = { − 1 , 0 , ⋯ ∣ t ∣ − 1 } l i n k \mathrm{link} l i n k
同时,我们定义 l e n ( u ) \mathrm{len}(u) l e n ( u ) u u u m i n l e n ( u ) \mathrm{minlen}(u) m i n l e n ( u )
l e n ( l i n k ( u ) ) + 1 = m i n l e n ( u ) \mathrm{len}({link}(u))+1=\mathrm{minlen}(u)
l e n ( l i n k ( u ) ) + 1 = m i n l e n ( u )
同时我们也可以得到一个等价类中包含的字符串的个数为 l e n ( u ) − m i n l e n ( u ) \mathrm{len}(u)-\mathrm{minlen}(u) l e n ( u ) − m i n l e n ( u )
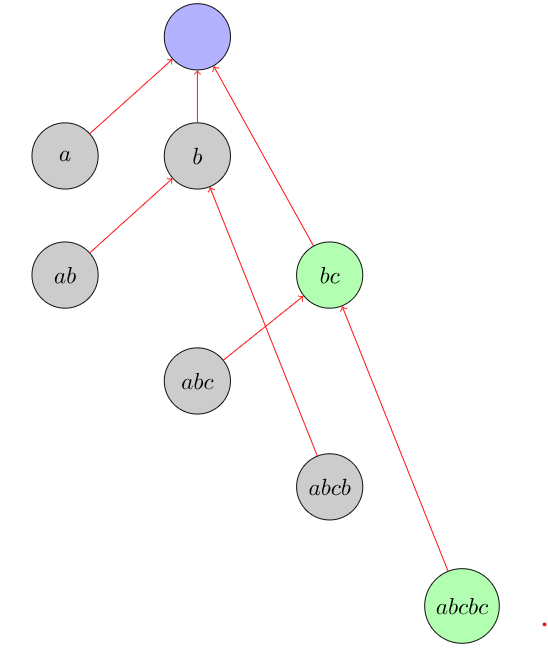
根据我们上面说的这些,我们构建出来的一棵树就叫做 Parent Tree。
下图是根据字符串 abcbc \texttt{abcbc} abcbc
我们可以证明,Parent Tree 中点的个数的数量级为 O ( n ) O(n) O ( n )
上面我们介绍了 Parent Tree,我们这里就要利用 Parent Tree 来构建 SAM。
SAM 的构建是在线算法,也就是说,我们可以每加入一个字符然后就进行扩展自动机。
这里先把构建的全过程放在这里:
首先,SAM 初始状态为只有一个节点 0 0 0 t 0 t_0 t 0 l e n ( 0 ) = 0 , l i n k ( 0 ) = − 1 \mathrm{len}(0)=0, \mathrm{link}(0)=-1 l e n ( 0 ) = 0 , l i n k ( 0 ) = − 1
设 l a s t last l a s t c c c 0 0 0 l a s t last l a s t
创建新状态 c u r cur c u r l e n ( c u r ) = l e n ( l a s t ) + 1 \mathrm{len}(cur)=\mathrm{len}(last)+1 l e n ( c u r ) = l e n ( l a s t ) + 1
接下来遍历 l a s t last l a s t c c c c c c
如果到达了虚拟状态 − 1 -1 − 1 l i n k ( c u r ) = 0 \mathrm{link}(cur)=0 l i n k ( c u r ) = 0
否则设第一个有 c c c p p p p p p c c c q q q
如果 l e n ( q ) = l e n ( p ) + 1 \mathrm{len}(q)=\mathrm{len}(p)+1 l e n ( q ) = l e n ( p ) + 1 l i n k ( c u r ) = q \mathrm{link}(cur)=q l i n k ( c u r ) = q
否则则进入最麻烦的情况:
我们对 q q q c o p y copy c o p y q q q c o p y copy c o p y l e n ( c o p y ) = l e n ( p ) + 1 \mathrm{len}(copy)=\mathrm{len}(p)+1 l e n ( c o p y ) = l e n ( p ) + 1
然后我们把 l i n k ( q ) \mathrm{link}(q) l i n k ( q ) l i n k ( c u r ) \mathrm{link}(cur) l i n k ( c u r ) c o p y copy c o p y
最后我们再从 p p p q q q c o p y copy c o p y q q q
最后,令 l a s t last l a s t c u r cur c u r
算法的正确性证明我不会/kk,所以我再把 OIWIKI 的讲解赫到这里/kel。
正确性证明
若一个转移 ( p , q ) (p,q) ( p , q ) len ( p ) + 1 = len ( q ) \operatorname{len}(p)+1=\operatorname{len}(q) l e n ( p ) + 1 = l e n ( q ) 连续的 。否则,即当 len ( p ) + 1 < len ( q ) \operatorname{len}(p)+1<\operatorname{len}(q) l e n ( p ) + 1 < l e n ( q ) 不连续的 。从算法描述中可以看出,连续的、不连续的转移是算法的不同情况。连续的转移是固定的,我们不会再改变了。与此相反,当向字符串中插入一个新的字符时,不连续的转移可能会改变(转移边的端点可能会改变)。
为了避免引起歧义,我们记向 SAM 中插入当前字符 c c c s s s
算法从创建一个新状态 cur \textit{cur} cur s + c s+c s + c
在创建一个新的状态之后,我们会从对应整个字符串 s s s c c c cur \textit{cur} cur c c c
最简单的情况是我们到达了虚拟状态 − 1 -1 − 1 s s s c c c c c c s s s cur \textit{cur} cur 0 0 0
第二种情况下,我们找到了现有的转移 ( p , q ) (p,q) ( p , q ) 已经存在的 字符串 x + c x+c x + c x x x s s s x + c x+c x + c s s s s s s cur \textit{cur} cur x + c x+c x + c len \operatorname{len} l e n len ( p ) + 1 \operatorname{len}(p)+1 l e n ( p ) + 1 len ( q ) > len ( p ) + 1 \operatorname{len}(q)>\operatorname{len}(p)+1 l e n ( q ) > l e n ( p ) + 1 q q q
如果转移 ( p , q ) (p,\,q) ( p , q ) len ( q ) = len ( p ) + 1 \operatorname{len}(q)=\operatorname{len}(p)+1 l e n ( q ) = l e n ( p ) + 1 cur \textit{cur} cur q q q
否则转移是不连续的,即 len ( q ) > len ( p ) + 1 \operatorname{len}(q)>\operatorname{len}(p)+1 l e n ( q ) > l e n ( p ) + 1 q q q len ( p ) + 1 \operatorname{len}(p)+1 l e n ( p ) + 1 s + c s+c s + c s s s q q q len ( p ) + 1 \operatorname{len}(p)+1 l e n ( p ) + 1 复制 状态 q q q clone \textit{clone} clone len ( clone ) \operatorname{len}(\textit{clone}) l e n ( clone ) len ( p ) + 1 \operatorname{len}(p)+1 l e n ( p ) + 1 q q q q q q clone \textit{clone} clone clone \textit{clone} clone q q q q q q clone \textit{clone} clone cur \textit{cur} cur clone \textit{clone} clone q q q clone \textit{clone} clone w + c w+c w + c w w w p p p p p p − 1 -1 − 1 q q q
根据上面的构造方法,我们还能证明,自动机中的节点数的量级为 O ( n ) O(n) O ( n )
构建方法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 inline void extend (char *s) int n = strlen (s + 1 ); for (int i = 1 ; i <= n; i ++ ) { int p = last, cur = ++ idx, c = s[i] - 'a' ; f[cur] = siz[cur] = 1 ; len[cur] = len[p] + 1 ; while (p != -1 && !tr[p][c]) { tr[p][c] = cur; p = link[p]; } if (p == -1 ) link[cur] = 0 ; else { int q = tr[p][c]; if (len[q] == len[p] + 1 ) link[cur] = q; else { int copy = ++ idx; len[copy] = len[p] + 1 ; link[copy] = link[q]; for (int i = 0 ; i < 26 ; i ++ ) tr[copy][i] = tr[q][i]; while (p != -1 && tr[p][c] == q) { tr[p][c] = copy; p = link[p]; } link[cur] = link[q] = copy; } } last = cur; } for (int i = 1 ; i <= idx; i ++ ) G[link[i]].emplace_back (i); }
注意 :SAM 中节点数最多能够达到 2 n − 1 2n-1 2 n − 1
【模板】后缀自动机(SAM)
给定一个只包含小写字母的字符串 S S S S S S 1 1 1
数据范围:∣ S ∣ ≤ 1 0 6 |S| \le 10^6 ∣ S ∣ ≤ 1 0 6
模板题。我们先建出 SAM,然后在 Parent Tree 上进行 DP。u u u
时间复杂度 O ( n ) O(n) O ( n )
[JSOI2012] 玄武密码
给定 n n n t t t t t t p p p p p p s s s
数据范围:∣ s ∣ ≤ 1 0 7 , ∑ ∣ t ∣ ≤ 1 0 7 |s|\le 10^7, \sum |t|\le 10^7 ∣ s ∣ ≤ 1 0 7 , ∑ ∣ t ∣ ≤ 1 0 7 4 4 4
SAM 裸题。由于 SAM 上存储了所有后缀的前缀,因此我们直接把 t t t
时间复杂度 O ( n ) O(n) O ( n )
[TJOI2015] 弦论
对于一个给定的长度为 n n n k k k
这里有两种询问:不同位置的相同子串算作一个和不同位置的相同子串算作多个。
数据范围:n ≤ 1 0 5 n\le 10^5 n ≤ 1 0 5
大杂烩题目,感觉像两道题拼起来的。
我们先考虑不同位置相同子串算一个的情况。这时我们可以先 dp,由于 SAM 为一张 DAG,因此我们可以记录从某个点开始走一共会走出多少种字符串。然后输出方案时,我们从小到大遍历出边,同时减去走这条边的方案数。直到 k k k
而对于不同位置算多个的,我们可以先按照上面模板题 的思路,先统计出每个点出现的次数,然后按照上面的重新 dp 即可。
Longest Common Substring
输入两个字符串,输出它们的最长公共子串长度。
数据范围:∣ s ∣ , ∣ t ∣ ≤ 2.5 × 1 0 5 |s|, |t|\le 2.5\times 10^5 ∣ s ∣ , ∣ t ∣ ≤ 2 . 5 × 1 0 5
我们先对一个串建 SAM,然后把另一个串放到 SAM 上跑。由于后缀链接记录的是前缀的后缀,因此跑不了的时候我们就一直跳后缀链接,同时记录一个最大长度即可。
时间复杂度 O ( n ) O(n) O ( n )
[AHOI2013] 差异
给定一个长度为 n n n S S S T i T_i T i i i i
∑ 1 ⩽ i < j ⩽ n l e n ( T i ) + l e n ( T j ) − 2 × l c p ( T i , T j ) \sum_{1\leqslant i<j\leqslant n}\mathrm{len}(T_i)+\mathrm{len}(T_j)-2\times\mathrm{lcp}(T_i,T_j)
1 ⩽ i < j ⩽ n ∑ l e n ( T i ) + l e n ( T j ) − 2 × l c p ( T i , T j )
数据范围:n ≤ 5 × 1 0 5 n\le 5\times 10^5 n ≤ 5 × 1 0 5
前面两项好搞,我们先提出来。这样我们的目标就变为了求 ∑ 1 ⩽ i < j ⩽ n l c p ( T i , T j ) \sum_{1\leqslant i<j\leqslant n}\mathrm{lcp}(T_i,T_j) ∑ 1 ⩽ i < j ⩽ n l c p ( T i , T j )
lcp 不好求,但是 SAM 适合求 lcs,我们就把字符串翻转过来,就变成了求 lcs。一个结论:i i i j j j l c a lca l c a l e n \mathrm{len} l e n l c a lca l c a
时间复杂度 O ( n ) O(n) O ( n )
Yet Another LCP Problem
给定一个字符串,每次询问的时候给出两个正整数集合 A A A B B B ∑ i ∈ A , j ∈ B l c p ( i , j ) \sum_{i \in A,j \in B}lcp(i,j) ∑ i ∈ A , j ∈ B l c p ( i , j )
数据范围:∣ s ∣ ≤ 2 × 1 0 5 , ∑ ∣ A ∣ , ∑ ∣ B ∣ ≤ 2 × 1 0 5 |s|\le 2\times 10^5, \sum |A|, \sum |B|\le 2\times 10^5 ∣ s ∣ ≤ 2 × 1 0 5 , ∑ ∣ A ∣ , ∑ ∣ B ∣ ≤ 2 × 1 0 5
我们先把字符串翻转,将 l c p lcp l c p l c s lcs l c s l e n len l e n
但是这里有多组询问,我们就可以每组询问建虚树,然后在虚树上进行 dp 计算答案。具体的说,我们设 s u m u , 0 sum_{u, 0} s u m u , 0 u u u A A A s u m u , 1 sum_{u, 1} s u m u , 1 u u u B B B a ∈ A , b ∈ B a\in A, b\in B a ∈ A , b ∈ B u u u l e n u len_u l e n u
时间复杂度 O ( n log n ) O(n\log n) O ( n log n )
[NOI2018] 你的名字
给定一个字符串 S S S T T T T T T S [ l ∼ r ] S[l\sim r] S [ l ∼ r ]
数据范围:∣ S ∣ ≤ 5 × 1 0 5 , ∑ ∣ T ∣ ≤ 1 0 6 |S|\le 5\times 10^5, \sum |T|\le 10^6 ∣ S ∣ ≤ 5 × 1 0 5 , ∑ ∣ T ∣ ≤ 1 0 6
我们先考虑 L = 1 , R = ∣ S ∣ L=1, R = |S| L = 1 , R = ∣ S ∣ S S S T T T T T T i i i S S S T T T i i i l i n k link l i n k
最后我们将每一个前缀的满足上面要求的最长后缀记录为 l i m i lim_i l i m i i i i t a g i tag_i t a g i
∑ p = 1 i d x max ( 0 , l e n ( p ) − max ( l e n ( l i n k ( p ) ) , l i m t a g p ) ) \sum \limits_{p=1}^{idx}\max(0, \mathrm{len}(p)-\max(\mathrm{len}(\mathrm{link}(p)), lim_{tag_p}))
p = 1 ∑ i d x max ( 0 , l e n ( p ) − max ( l e n ( l i n k ( p ) ) , l i m t a g p ) )
也就是对于每个节点,我们用它的长度减去它匹配的长度就是它不为 S S S
而对于有了区间限制这个东西,我们可以思考一下我们上面用 SAM 都做了什么:跳 l i n k link l i n k e n d p o s \mathrm{endpos} e n d p o s
而对于 e n d p o s \mathrm{endpos} e n d p o s
时间复杂度 O ( n log n ) O(n\log n) O ( n log n )
区间本质不同子串个数
给定一个长度为 n n n S S S m m m S S S L L L R R R
数据范围:n ≤ 1 0 5 , m ≤ 2 × 1 0 5 n\le 10^5, m\le 2\times 10^5 n ≤ 1 0 5 , m ≤ 2 × 1 0 5
对于区间数不同颜色这种问题,一个常见的套路为讲询问离线,然后右端点扫描线,同时只维护每个不同元素在最右端出现的位置。
而对于这题我们也可以这么做。我们把询问离线后做扫描线,发现每次新加入的元素的 e n d p o s \mathrm{endpos} e n d p o s
我们就可以沿用[SDOI2017] 树点涂色 的套路,用 LCT 来维护这个过程。具体地说,我们在 LCT 的每个点维护一个 v a l val v a l e n d p o s \mathrm{endpos} e n d p o s v a l val v a l
时间复杂度 O ( n log 2 n ) O(n\log^2n) O ( n log 2 n )
说着很麻烦但是写起来都是板子反而相当好写/yiw
其实 SAM 还有很多东西没讲完,但是限于作者本人能力问题,有很多应用和证明都没有讲。以后可能会再更新一点。
参考资料:OIWIKI -https://oi-wiki.org/string/sam/