最近写了一些 AGC 的题，都还不错，整理一下。持续更新。
AGC001E
有 $n$ 个数对 $(a_i, b_i)$，求出
$$
\sum_{i=1}^{n}\sum_{j=i + 1}^{n}\dbinom{a_i+b_i+a_j+b_j}{a_i+a_j}
$$
数据范围：$n\le 10^5, a_i, b_i\le 2000$。
首先显然我们要求的式子可以转化为求 $\sum_{i=1}^{n}\sum_{j=1}^{n}\dbinom{a_i+b_i+a_j+b_j}{a_i+a_j}$ 我们要求的我们可以上来暴力推式子，但是我们可以考虑考虑组合意义。
显然，从 $(0, 0)$ 走到 $(x, y)$ 的方案数为 $\dbinom{x+y}{x}$。因此 $\dbinom{a_i+b_i+a_j+b_j}{a_i+a_j}$ 即为从 $(0, 0)$ 走到 $(a_i+a_j, b_i+b_j)$ 的方案数。但是这样转化我们还是需要两两枚举点，复杂度为 $O(n^2)$。
但是我们可以注意到题目里 $a_i\le 2000$，因此我们可以进行一个 $O(a_i^2)$ 的东西。我们考虑把上面的式子中起点和终点参数分离一下，我们可以直接把我们走的矩形区域平移一下，我们就可以得到 $\dbinom{a_i+b_i+a_j+b_j}{a_i+a_j}$ 的新的意义：从 $(-a_i, -b_i)$ 走到 $(a_j, b_j)$ 的方案数。我们发现可以把所有起点都加入到平面内，然后进行一个 dp。最终枚举终点统计即可。
时间复杂度 $O(a^2)$。
AGC002E
桌上有 $n$ 堆糖果，第 $i$ 堆糖果有 $a_i$ 个糖。两人在玩游戏，轮流进行，每次进行下列两个操作中的一个:
将当前最大的那堆糖果全部吃完；
将每堆糖果吃掉一个；
吃完的人输，假设两人足够聪明，问谁有必胜策略？
数据范围：$1\leq n\leq10^5$，$1\leq a_i\leq10^9$。
我们可以先把糖果排个序，这样我们就可以把问题转化到一个二维平面上去。
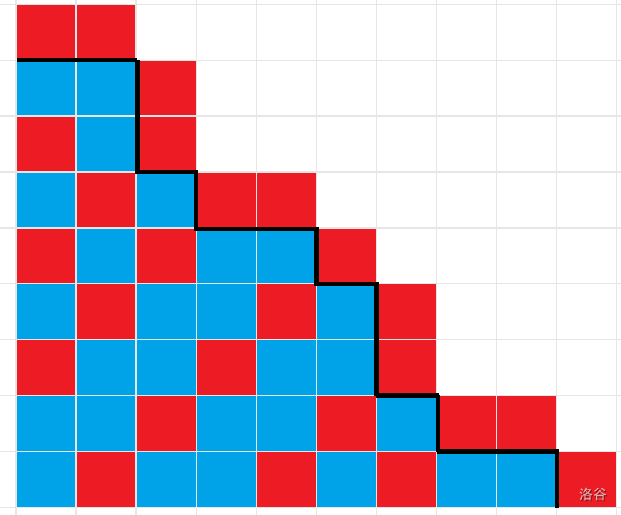
图中黑色的线即为糖果的边界。我们从左下角出发，执行吃掉最大的一堆就可以看作是向右走，全部吃掉一个就可以看作是向上走。吃完的人输也就是走出地图边界的状态为必败态。
我们就可以把所有位置的输赢状态标到图上（红色为必败，蓝色为必胜），我们就可以发现一个对角线上都是相同的状态。但是我们只关注起点的状态，我们就可以从起点出发，向右上方走，走到头不能走后我们判断其为必胜还是必败即可。
时间复杂度 $O(n)$。
AGC003D
给定 $n$ 个数 $s_i$，要求从中选出最多的数，满足任意两个数之积都不是完全立方数。
数据范围：$n\le 10^5$，$s_i\le 10^{10}$。
我们发现这个数据范围甚至不允许我们进行常规的质因数分解。但是题目中说的是完全立方数，我们可以从三次根号这里下手。
我们可以先把一个数的所有质因子的次数 $\bmod 3$，这样我们就可以为一个数找到另一个和它不能配对的数了，而且这两个数不影响其它的数字选择。如果我们对所有的数都找到和它冲突的数，我们就能很简单地得到最终答案。
现在问题就是如何找到和它冲突的数。我们可以先把 $a_i$ 小于 $\sqrt[3]{10^{10}}$ 的质因子全部除掉，设剩下的数为 $c$。当 $c\le (10^{10})^{\frac{2}{3}}$ 时，我们发现 $c$ 只有可能是一个质数 $p$，否则它就会有一个小于等于 $\sqrt[3]{10^{10}}$ 的质因子。
而当 $c> (10^{10})^{\frac{2}{3}}$ 时，我们发现 $c$ 只有三种可能：$p$、$pq$、$p^2$（$p,q$ 都为质数）。而当 $c=p$ 或 $c=pq$ 时，它所对应的不能选择的数字一定就有一个约数 $p^2$ 或 $p^2q^2$，但是我们发现这两种情况都会爆掉 $10^{10}$ 的限制，因此我们只需要判断 $c$ 是否为完全平方数即可。
时间复杂度 $O(n\sqrt[3]{n}+n\log n)$。
AGC003E
一串数，初始为 $1\sim n$，现在给 $Q$ 个操作，每次操作把数组长度变为 $a_i$，新增的数为上一个操作后的数组的重复。问 $Q$ 次操作后 $1\sim n$ 每个数出现了多少次。
数据范围：$n, Q\le 10^5, a_i\le 10^{18}$。
首先我们手玩一下可以发现，如果当 $a_{i}>a_{i+1}$ 时，我们所做的第 $i$ 次操作是无用的，因为它最后也会被 $a_{i+1}$ 给缩回去。因此我们先用单调栈把 $a$ 处理成上升序列。
我们发现进行一次扩展，增加的数是在原来的数字基础上乘以 $\left \lfloor \frac{a_{i+1}}{a_i} \right \rfloor$，以及最后 $a_{i+1}\bmod a_i$ 的边角料。如果没有边角料的话，我们直接记录一个乘的系数即可。而对于这些边角料（设其长度为 $d$），我们找一下它是从哪来的。
如果我们找到一个 $j$ 使得 $a_j\le d$ 并且 $a_{j+1}>d$ 时，我们发现 $d$ 关于 $a_j$ 的关系和 $a_i$ 关于 $a_{i+1}$ 的关系一样，都是重复一些之后再多一些边角料。我们就可以对 $d\bmod a_j$ 递归处理。递归到无法找到满足条件的 $j$ 时就意味着 $1\sim d$ 这些数在最后剩下的边角料中都再出现了一次。因此我们直接对这些数的出现次数差分一下即可。
同时为了得到边角料的重复次数，我们可以从后往前进行递推。
每次 $d$ 至少会减半，因此复杂度为 $O(n\log^2n)$。
AGC003F
给定一个 $n\times m$ 的网格。每个单元格都是黑色或白色。所有黑色单元格都是四联通的。
第 $i$ 行第 $j$ 列 $(1\le i\le n,1\le j\le m)$ 的单元格的颜色由字符 $s_{ij}$ 表示。如果 $s_{ij}$ 是 #，该单元格为黑色；如果 $s_{ij}$ 是 .，该单元格为白色。至少一个单元格是黑色的。
我们定义「$n$ 级分形」如下：$0$ 级分形是一个 $1\times1$ 的黑色单元格。$n$ 级分形由 $n-1$ 级分形变化而来。具体地，将 $n-1$ 级分形的每一个黑色单元格替换为给定的网格，每一个白色单元格替换为与给定的网格尺寸相同的全部为白色的网格，就成了 $n$ 级分形。
求出 $K$ 级分形中，有多少个黑色格子组成的四联通块？
数据范围：$n, m\le 1000, k\le10^{18}$。
我们手玩几组数据可以发现，原图如果上面和下面连通（存在 $i$ 使得 $s_{i, 1}=s_{i, m}$）并且左边和右边连通（同上），那么不管我们做几次分形，最终的图案一定只会有一个连通块。
而对于上下和左右都不连通的图案，假如我们设一共有 $a$ 个黑点，那么显然最终答案就是 $a^{k-1}$，因为每次我们都会让一个黑格变为一个连通块。
现在我们只剩下初始图案上下连通或者左右连通的情况了。显然上下联通可以翻转而转化为左右联通，因此我们只需要解决左右联通的问题。我们考虑 dp。
我们设 $f_i$ 为第 $i$ 次分形时连通块的数量，$a$ 为初始图案黑点数量。当第 $i$ 次分形时，我们发现我们展开两个上下相邻的黑点时，它们不会互相干扰，而对于左右相邻的黑点，则会使连通块数量比 $af_{i-1}$ 减少。因此我们设第 $i$ 次分形时左右相邻的黑点数量为 $s_i$，原图左右相邻的黑点数为 $b$，那么我们可以得到：
$$
f_i=af_{i-1}-bs_{i-1}
$$
而对于 $s$ 的递推，我们可以发现，使得相邻黑点增加的来源只有分形展开时原图案的右侧和左侧会产生新的贡献，因此我们设 $c$ 为满足一行的最左侧和最右侧都为黑色格子的行数（也就是满足 $s_{i, 1}=s_{i, m}$ 的 $i$ 的数量）。那么就可以得到 $s$ 的递推式：
$$
s_{i}=cs_{i-1}
$$
对于 $k\le 10^{18}$，我们可以直接进行一个矩阵快速幂。
时间复杂度 $O(nm+\log k)$。
Salvage Robots
有一个 $n\times m$ 的棋盘，上面要么是空的，要么有一个机器人，要么是一个出口（整个地图只有一个出口）。每次可以命令所有机器人向上下左右中的某个方向移动一格，如果它超出了棋盘的边界就会消失。如果它到了出口的位置就会被你救下（并且从棋盘上消失）。求你能够救下的机器人的最大值。
数据范围：$n, m\le 100$。
我们可以转换参考系，我们把机器人整体挪动换为出口在挪动，那么我们可以发现：出口的移动范围一定是个矩形，因为如果不是矩形的话，我们可以把边角上的缺口补上，同时也不会使得多余的机器人死亡。
我们设出口已经向上移动过了 $u$，向下移动过了 $d$，向左移动了 $l$，向右移动了 $r$ 时能拯救的机器人数量最大为 $f_{u, d, l, r}$，我们考虑如何转移。
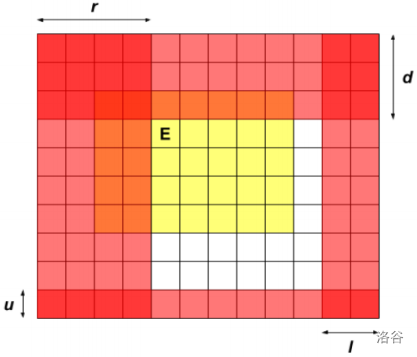
上图中，红色+白色的部分是已经死过的，而有黄色的部分是出口走过的地方，这里我们已经处理过，不用考虑，我们只需要考虑没有被红色覆盖的白色部分。我们可以对上面的状态进行上下左右四个方向的扩展，如下图：
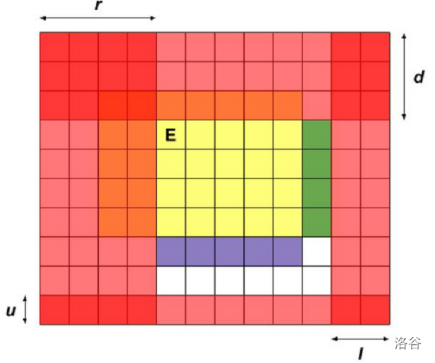
我们就可以写出上图的转移方程：
$$
f_{l, r + 1, u, d}\leftarrow f_{l, r, u, d}+sum_{green}
$$
$$
f_{l, r, u, d + 1}\leftarrow f_{l, r, u, d}+sum_{purple}
$$
而对于剩下两个方向的扩展也是同理。而对于 $sum$，我们可以直接前缀和优化。
时间复杂度 $O(n^4)$。
~K Perm Counting
如果一个排列 $p$ 满足对于所有的 $i$ 都有 $|p_i-i|\neq k$，则称排列 $p$ 为合法的。现给出 $n$ 和 $k$，求有多少种合法的排列。
数据范围：$2\leq n\leq 2\times 10^3$，$1\leq k\leq n-1$。
我们先进行一个二项式反演，我们直接钦定有 $j$ 个位置满足 $|p_i-i|=k$，我们设放置 $j$ 个 $|p_i-i|=k$ 的 $p_i$ 的方案数为 $g_j$。那么最终答案为：
$$
ans=\sum_{i=0}^n (-1)^i\times g_i\times (n-i)!
$$
现在我们要求的就是 $g_j$。我们将图分为左部和右部，其中左部为下标，右部为值，将左部的 $i$ 和右部的 $i\pm k$ 连边，最终得到的图一定是一堆链。我们的目标就是选出 $j$ 条边并且使得两条边没有公共顶点。
我们可以把这堆链先首尾相连方便 dp。我们设 $f_{i, j, 0/1}$ 为前 $i$ 条边选了 $j$ 条，同时第 $i$ 条边是否选择的方案数，那么我们有转移：
$$
f_{i, j, 0}=f_{i-1, j, 0}+f_{i-1, j, 1}
$$
而当 $i$ 是链顶时，它不存在 $f_{i, j, 1}$。当 $i$ 不是链顶时，转移有：
$$
f_{i, j, 1}=f_{i-1, j-1, 0}
$$
最终 $g_{i}$ 就为 $f_{n\times 2, i, 0}+f_{n\times 2, i, 1}$。
另一种求法：
我们对每条链分别处理，$i$ 个物品中选 $j$ 个不相邻物品的方案数为 $\dbinom{i-j+1}{j}$，那么我们把它的 OGF 写出来后，对每条链所对应的 OGF 进行一个卷积即为我们要求的 $G(x)$。
时间复杂度 $O(n^2)$ 或 $O(n\log n)$。
AGC005E
现在 A（crimson000） 和 B（Koishi） 在玩游戏，游戏是在两棵树上进行的，A 在树 $a$ 上的点 $x$，B 在树 $b$ 上的点 $y$，两棵树上的点的编号是相同的，只是连边方式不同。
对于奇数轮，A 可以选择走到它当前在树 $a$ 上的点的相邻节点，或者在原地不动，对于偶数轮则是 B 进行选择，当两个人到达编号相同的点时，游戏结束。
现在 A 想最大化游戏轮数，B 想最小化游戏轮数。问游戏的轮数，如果可以进行无限轮游戏，请输出 $-1$。
数据范围：$n\le 2\times 10^5$。
我们手玩样例可以得到判定无解的方案：在 $A$ 树中相邻的两个节点 $u, v$，其在 $B$ 树中的距离大于等于 $3$ 时则无解，因为 A 可以在 B 走到一个节点时走到另一个节点。
我们考虑完了无解情况，现在在无解之前，$B$ 树上所有相邻两点在 $A$ 树上距离不超过 $2$。我们把 $A$ 树中的边都加入到 $B$ 中，这些边都是只有 A 能走的边。我们发现 A 一定不会通过这些边来跨过 B，因为 A 现在一步最多只能沿 $A$ 树边跨两步，跨到 B 对面后一定会被 B 抓住，因此不如不跨过去。
我们处理出 $B$ 树以 $y$ 为根每个点的距离 $dep_u$，我们发现在 $A$ 树中距离 $x$ 为 $d$ 的点 $u$，当 $d\ge dep_u$ 时，A 必然不可能去走到 $u$，因为 A 在走到 $u$ 之前或者恰好走到 $u$ 时就会被 B 拦截住，因此 A 的活动范围即为所有 $d<dep_u$ 的点。我们再在这些点中找是否出现无解的情况。如果没有无解，那么 A 一定会选择在 $dep_u$ 最大的点等着 B 来追到 A，因此最终答案为 $\max(dep_u)\times 2$。
时间复杂度 $O(n)$。
AGC005F
给定一棵无根树，定义 $f(i)$ 为：对于所有大小为 $i$ 的点集 $S$，在原树上最小的包含 $S$ 中所有点的最小连通块的大小之和。对于所有 $i=1\cdots n$，求出 $f(i)$。
数据范围：$n\le 2\times 10^5$。
我们把贡献分散到每个点上。我们考虑一个点 $u$ 有多少时候会不在这个连通块中：所有 $S$ 中的点都在 $u$ 的一个儿子的子树中。因此我们可以得到 $u$ 对 $f(i)$ 的贡献：
$$
\dbinom{n}{i}-\sum {v\in son_u}\dbinom{siz_v}{i}
$$
因此
$$
\begin{aligned}
f(i)&=\sum{u=1}^n\left( \dbinom{n}{i}-\sum\limits_{v\in son_u}\dbinom{siz_v}{i} \right)\
&=n\times \dbinom{n}{i}-\sum_{u=1}^n\sum_{v\in son_u} \dbinom{siz_v}{i}
\end{aligned}
$$
我们设 $cnt_i$ 为对于所有 $u$，子树大小为 $i$ 的儿子数量之和。那么我们就能把上面式子再化简：
$$
\begin{aligned}
f(i)&=n\times \dbinom{n}{i}-\sum_{j=i}^n cnt_j\times \dbinom{j}{i}\
&=n\times \dbinom{n}{i}-\sum_{j=i}^n cnt_j\times \frac{j!}{i!(i-j)!}\
&=n\times \dbinom{n}{i}-\frac{1}{i!}\sum_{j=i}^n cnt_j\times \frac{j!}{(i-j)!}
\end{aligned}
$$
我们构造多项式 $F(x)=\sum cnt_i\times i!\times x^i$，$G(x)=\sum \frac{1}{i!}x^i$。那么 $f(i)=n\times \dbinom{n}{i}-\frac{1}{i!}\sum_{j=i}^n F_{j}\times G_{i-j}$。
显然后面是个差卷积，NTT 即可。
时间复杂度 $O(n\log n)$。
AGC006C
有 $n$ 只兔子在一个数轴上，兔子为了方便起见从 $1$ 到 $n$ 标号，第 $i$ 只兔子的初始坐标为 $x _ i$。 兔子会以以下的方式在数轴上锻炼：一轮包含 $m$ 个跳跃，第 $j$ 次跳跃是兔子 $a _ j(2\le a_j\le n-1)$ 跳一下，这一下从兔子 $a _ j - 1$ 和兔子 $a _ j + 1$ 中等概率的选一个。假设选了 $x$，那么 $a _ j$ 号兔子会跳到它当前坐标关于 $x$ 的坐标的对称点。 （即使兔子的位置顺序变化了，但是编号仍保持不变，这里按兔子编号算） 兔子会进行 $k$ 轮跳跃，对每个兔子，请你求出它最后坐标的期望值。
数据范围：$n\le 10^5, k\le 10^{18}$。
显然我们可以得到 $a_i$ 在一次跳跃后的期望位置，我们设 $x_i$ 为 $i$ 当前的期望位置，则有：
$$
x_{a_i}\leftarrow \frac{1}{2}(2\times x_{a_i+1}-x_{a_i})+\frac{1}{2}(2\times x_{a_i-1}-x_{a_i})
$$
$$
x_{a_i}\leftarrow x_{a_{i+1}}+x_{a_{i-1}}-x_{a_i}
$$
我们发现这个式子其实就是交换相邻两项的差分。因此我们可以记录差分，记录一轮后每个位置上的差分跑到哪了，然后进行一个置换快速幂即可。
时间复杂度 $O(n\log k)$。
AGC006D
给出一个 $n$ 层的方格金字塔，自顶向下依次标号为第 $1$ 到第 $n$ 层。 其中第 $i(1 \le i \le n)$ 层有 $2i - 1$ 个方格。（见下图） 第 $n$ 层有一个 $1$ 到 $2n-1$ 的排列，其他层的数字按以下规则生成：方格 $b$ 中填写的整数，是方格 $b$ 正下方、左下方和右下方方格中所写整数的中位数。 现在给出第 $n$ 层的数字，请你求第一层的数字。
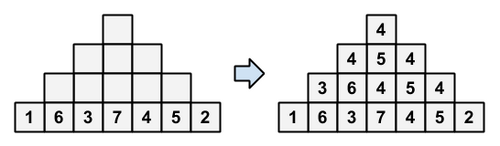
数据范围：$n\le 10^5$。
我们可以按照这题的思路，我们对最上面的中位数进行一个二分。我们把大于 $mid$ 的数设为 $1$，其余数设为 $0$。我们可以发现，如果有两个相邻的 $1$ 比两个相邻的 $0$ 距离中点更近，那么最上面的数一定会是 $1$。对于两个相邻的 $0$ 同理。
而如果没有相邻的相同数字，那么手玩可以发现：决定最上面数字的是中点上的数字。
时间复杂度 $O(n\log n)$。
AGC006F
我们有一个 $n$ 行 $n$ 列的矩阵。第 $i$ 行第 $j$ 列的格子表示为 $(i,j)$。
开始时，有 $m$ 个格子是黑色，其他格子都是白色。特别地，开始时格子 $(a_{1},b_{1}),(a_{2},b_{2}),\cdots, (a_{m},b_{m})$ 是黑色。
crimson000 会按照以下的规则尽可能多的将白色格子涂成黑色：
- 对于整数 $1\le x,y,z\le n$，如果 $(x,y)$ 和 $(y,z)$ 都是黑色，那么就把 $(z,x)$ 涂黑。
请计算出当再也没有白色格子能被涂黑时，黑色格子的个数。
数据范围：$n, m\le 10^5$。
我们考虑如果有 $(x, y)$ 这个点，那么我们直接连一条 $x$ 指向 $y$ 的边。我们就能把题目的条件转化为：如果存在 $x\to y$ 和 $y\to z$ 这两条边，那就有 $z\to x$ 这条边。
我们考虑对原图进行一个三染色，我们把每一个连通块分开来看：
当一个连通块可以被三染色，但是只染了两种或一种颜色时，我们可以得到结论不存在 $x\to y\to z$ 的边，那么这个连通块的贡献只有它原来的边数。
当一个连通块不能被三染色，那么我们可以证明，它的贡献是 $siz^2$。这里不再具体证明。
而当一个连通块恰好能被三染色，那么它的贡献就是 $cnt_0\times cnt_2+cnt_1\times cnt_0+cnt_2\times cnt_1$。也就是一个点出发再走两步的贡献。
时间复杂度 $O(n)$。
AGC007C
在一条直线上有 $n$ 个球和 $n+1$ 个洞。记每个球与相邻的洞的距离为 $d_i \left( 1 \leq i \leq 2 \times n \right)$ 且 $d_{i + 1} - d_i = x$。
要将 $n$ 个球均推入洞中。当球滚过洞时，如果洞中还没有球，球将掉入洞中。否则，球将继续滚动。
每次会随机选择任一未进洞的球，并随机选择一个方向推球。
给定 $n, d_1, x$ ，求出在不发生碰撞的情况下，每个球移动距离的期望。
数据范围：$n\le 2\times 10^5$。
我们发现题目中给定的这些距离形成了一个等差数列。那么显然我们在所有距离都是一个等差数列时，我们推一次球移动的期望距离是这个等差数列的中位数。那么现在我们目标就是算出每次推球之后这个 $d$ 会如何变化。
我们考虑第 $i$ 段距离在一次推球后会如何变化。一共有 $2n$ 种推球的可能，当第 $i$ 段之前的球被推时，第 $i$ 段的距离将会变为第 $i+2$ 段。而当第 $i+1$ 段被滚时，第 $i$ 段的距离将会变为 $d_{i}+d_{i+1}+d_{i+2}$。这里可以画图理解。那么我们就能得到下面的式子：
$$
d_i\leftarrow d_i+\frac{i(d_{i+2}-d_i)+(d_{i+1}+d_{i+2}))}{2n}
$$
我们对后面进行一个化简，设 $d=d_1$，$x$ 为公差，那么我们稍微化简可以得到：
$$
d_i\leftarrow d_i+\frac{5x+2d}{2n}+\frac{2x}{n}i
$$
首项就变为了 $d+\frac{5x+2d}{2n}$，公差变为了 $\frac{2x}{n}$。就可以直接计算了。
时间复杂度 $O(n)$。
AGC007D
crimson000 在玩一个游戏。初始时他在数轴的 $0$ 位置，出口在 $E$ 位置，并且数轴上还有 $n$ 块石头，第 $i$ 块石头在 $x_i$ 位置。
crimson000 拿着 $n$ 个帽子出发，每走一个单位长度要花费一秒。到一块石头的位置时，他可以送给这个石头一个帽子，这个过程不花时间。小石头收到帽子后，$T$ 秒以后会在它所在的位置产生一把刀。
crimson000 想知道，他从出发到收集了所有刀抵达出口，最少要花费多长时间。
数据范围：$n\le 10^5$。
我们发现我们的最优决策一定是先往前走，走到一定程度之后返回来把产生的刀给拿了。因此我们设 $f_i$ 为拿了前 $i$ 把刀所需要的最小时间，那么我们就可以进行一个 dp。
$$
f_i=\min (f_j+x_i-x_j+\max (2\times (x_i-x_{j+1}), T))
$$
我们发现里面 $x_i-x_j$ 这项到最后也就只是一个 $E$，我们可以直接不管它，最后加上 $E$ 即可。然后我们就要考虑后面 $\max (2\times (x_i-x_{j+1}), T)$ 这一项了。
我们进行一个分类讨论。当 $2\times (x_i-x_{j+1})\ge T$ 时，我们找到第一个满足不这个条件的 $j$，我们记为 $l$。我们发现 $x_i$ 是单调递增的，因此我们的 $l$ 也必然是单调不降的，因此直接双指针维护即可。同时我们维护在 $l$ 之前的所有 $f_j-2\times x_{j+1}$ 的最小值，转移就可以 $O(1)$ 转移了。而对于 $2\times (x_i-x_{j+1}) <T$ 时，我们可以发现 $f_i$ 必然是单调递增的，因此我们直接选取 $f_l$ 进行转移即可。
时间复杂度 $O(n)$。
AGC007F
crimson001 的工作是复制。有一天，crimson001 从他的上司 crimson000 那里拿到了一个由小写英文字母组成的长度为 $n$ 的字符串 $S_{0}$（假设这天是第 $0$ 天）。这之后第 $i$ 天的工作是把 $S_{i-1}$ 复制到 $S_{i}$。下文中的 $S_{i}[j]$ 表示字符串 $S_{i}$ 的第 $j$ 个字母。
crimson001 还不怎么习惯这个工作。每天，当 crimson001 从第一个字母开始按顺序复制字符串时，他有可能会写下和刚刚写下的字母相同的字母，而不是本来应该写下的字母。也就是说，$S_{i}[j]$ 要么与 $S_{i-1}[j]$ 相同，要么与 $S_{i}[j-1]$ 相同。（特别地，字符串开头的字母不可能出错。也就是说，$S_{i}[1]$ 必然与 $S_{i-1}[1]$ 相同。）
输入两个字符串 $S_{0}$ 和 $T$，请求出使得 $S_{i}$ 有可能与 $T$ 相同的最小的整数 $i$。
数据范围：$n\le 10^6$。
我们可以发现，我们每次进行区间覆盖，都是在前面找到一个匹配到的，然后等到它后面的覆盖完后它再紧跟着覆盖上。我们把这个流程画到图中：
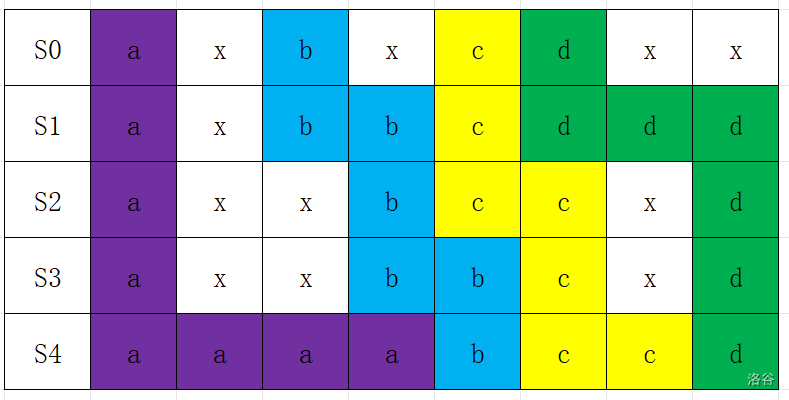
我们发现这些覆盖的路线形成了一条折线，通过贪心可以分析出来：折线需要尽可能地靠右走，这样才能给左边的折线留下更大的空隙。因此我们可以维护一个拐点的队列，每次加入点时弹出不会碰到的拐点，最后再把当前拐点加入。答案即为所有拐点（不算最后一行）的深度最大值加一。
时间复杂度 $O(n)$。
AGC008E
给定正整数 $n$ 和一个长度为 $n$ 的序列 $a$，问有多少长度为 $n$ 的排列 $p$，满足对于任意 $i$ 有 $p_i=a_i$ 或 $p_{p_i}=a_i$。
数据范围：$n \leq 10^5$。
我们先考虑给定 $p$ 能够构造出怎样的 $a$。我们先从 $i$ 向 $p_i$ 连边，那么就能形成一堆环。而 $a$ 的条件也就是一个点在 $a$ 构成的图中指向的点只能是在 $p$ 中第一个指向的点或指向的点的指向的点。那么我们考虑一个环能变成什么样子：
- 情况 1：$a_i=p_i$。这种情况这个环不会发生变化。如下图：
- 情况 2：$a_i=p_{p_i}$ 且环大小为奇数。这种情况会变成一个新环，但是会变成一个不一样的环，如下图：
- 情况 3：$a_i=p_{p_i}$ 且环大小为偶数。这种情况会把一个环分裂成两个环：
- 情况 4：既有 $a_i=p_i$ 也有 $a_i=p_{p_i}$，这种情况会变为一颗内向基环树。
但是我们现在已知的是 $a$ 构成的这张图，而不是 $p$，我们就考虑把 $a$ 复原回去。
我们先考虑简单环的情况，我们可以进行一个 dp。我们枚举环的大小 $i$，记录有 $sum$ 个大小为 $i$ 的环。我们设 $f_i$ 为考虑前 $i$ 个环的方案数，我们根据情况一二三就能得到转移方程：
$$
f_j \leftarrow \left{\begin{matrix}
2\times f_j \ \ \ (i\bmod 2 =1)\
f_j \ \ \ \ \ \ \ \ \ \ (i\bmod 2=0) \
(j-1)\times i\times f_{j-2} \ \ (j>1)
\end{matrix}\right.
$$
而对于基环树的情况，我们考虑把多出的链给塞进去。如果一个多出的链长度为 $l_1$，这个链顶到下一个有多出链的部分的长度为 $l_2$，那么：
- 当 $l_1<l_2$ 时这个链塞进去的方案数为 $0$。
- 当 $l_1=l_2$ 时这个链塞进去的方案数为 $1$。
- 当 $l_1>l_2$ 时这个链塞进去的方案数为 $2$。
塞链的过程可以看下图：
最后再把上面这些用乘法原理乘起来即可。
时间复杂度 $O(n)$。
AGC009C
给定 $n$ 个不同的整数，求将它们分成两个集合 $X,Y$，并且 $X$ 集合中任意两个数的差大于等于 $A$，$Y$ 集合中任意两个数的差大于等于 $B$ 的方案数。
数据范围：$n\le 10^5$。
为了方便，我们假设 $A\ge B$。
我们先来考虑无解的情况。当三个数出现两两之差都小于 $B$ 的情况时，一定无解，因为一定会有两个数分到同一个集合中。
接下来我们进行一个 dp。我们设 $f_i$ 为前 $i$ 个数全部放完，且第 $i$ 个数放到 $X$ 中的方案数。转移我们可以枚举 $j$，然后让 $j+1$ 到 $i-1$ 这段区间的数全部放到 $Y$ 中。因此我们的转移即为：
$$
f_i=\sum _{j<i}f_j
$$
同时我们还要求 $[j+1, i-1]$ 这段区间的数两两之差都大于等于 $B$，并且 $a_i-a_j$ 必须大于等于 $A$。不难发现有了这两个限制我们可转移的 $j$ 就形成了一段区间，并且这段区间的两个端点都是单调的，直接用两个指针+前缀和维护即可。
时间复杂度 $O(n)$。
AGC010C
一棵树，第 $i$ 个节点上有 $a_i$ 个石头，每次选择两个叶子节点（度数为 $1$ 的节点），将路径上经过的（包括起点终点）所有节点上都取走一个石头，如果路径上有一个点上没石头这个操作就不能进行，问能不能取完所有石头。
数据范围：$n\le 10^5$。
我们先选取一个度数不为 $1$ 的点为根。我们考虑一个点的石子都是如何被取走的：从它子树中选两个点，并且这两个点的 $lca$ 为它、它子树内选一个点，再在外面选一个点。
我们设 $f_u$ 为 $u$ 节点有多少石子是通过第二个方法取走的。我们设 $sum=\sum _{v\in son_u} f_v$，也就是 $u$ 的儿子一共要伸上来多少条路径，我们就在这些里面进行两两配对和向上传递。两两配对一次会让 $sum$ 减二，让 $a_u$ 减一。向上延伸一条路径会让 $sum-1$，让 $a_u$ 减一。因此我们可以得到等式：
$$
a_u=f_u+ \frac{sum-f_u}{2}
$$
我们就能得到 $f_u=2a_u-sum$。我们判定无解有三个条件：
- $f_{root}$ 必须为 $0$。这点是显然的，根节点不能再往上传递。
- $0\le f_u\le a_u$。这点也是显然的，向上传递的石子不能比它本身的石子还多。
- 设 $mx=\max _{v\in son_u}f_v$，那么 $mx\le \frac{sum-f_u}{2}$。关于这点，我们可以把 $f_v$ 看作一个序列，一共要进行 $\frac{sum-f_u}{2}$ 次操作，每次操作选择两个不同的数使其 $-1$。询问是否最终能使得这个序列全为 $0$。有关这个问题我们的结论是只要这个序列中最大值不超过总和的一半就可以。证明可以用归纳法证明。
时间复杂度 $O(n)$。
AGC010D
黑板上写着 $n$ 个整数。第 $i$ 个整数是 $a_i$ ，它们的最大公约数为 $1$ 。
crimson000 和 Koishi 将使用这些数来玩一个游戏。crimson000 在这个游戏中是先手，他们将轮流进行以下操作（以下两步相当于一次操作）：
- 选择黑板中大于 $1$ 的一个数，将其减 $1$ 。
- 此后，将黑板上所有数全部除以所有数的最大公约数。
当黑板上的数全部为 $1$ 时，不能再进行操作的人就失败了。两人都选择最好的方式行动，请求出哪边会最终胜利。
数据范围：$n\le 10^5, a_i\le 10^9$。
首先没有除以 $\gcd$ 的操作时，我们可以通过奇偶性来判断谁胜。而带上除以 $\gcd$ 操作时，可能就会翻盘。由于只有除以偶数的 $\gcd$ 才可能会改变和的奇偶性，我们肯定要对奇数和偶数下手。下面进行一个分类讨论：
- 当出现 $1$ 时，就相当于没有第二个操作了，直接判断奇偶性。如果场上有奇数个偶数，则先手必胜，否则后手必胜。
- 当场上有奇数个偶数时，先手只需要保持住当前的局面即可。先手可以取走一个偶数的 $1$，而后手无论如何取也会使得偶数的数量回归奇数。先手必胜。
- 当场上有偶数个偶数，且奇数的数量大于 $1$ 时，上面的情况就会转到后手，因此后手必胜。
- 而当场上仅有一个奇数，有偶数个偶数时，先手就可能可以翻盘。先手可以取走奇数，这时所有的数都会除去一个偶的 $\gcd$，剩下的摊子就留给后手去管。
这样前三个操作都是直接结束，最后一个操作会使所有数除以至少 $2$，求 $\gcd$ 的复杂度为 $O(\log n)$。因此复杂度为 $O(n\log^2 V)$。
AGC010F
有一棵 $n$ 个节点的树，第 $i$ 条边连接 $a_i,b_i$，每个节点 $i$ 上有 $a_i$ 个小石头，crimson000 和 Flandre 将在树上玩游戏。
首先，crimson000 会选一个节点并在上面放一个棋子，然后从 crimson000 开始，他们轮流执行以下操作：
- 从当前棋子占据的点上移除一个小石头
- 将棋子移动到相邻节点。
如果轮到一个人执行操作时棋子占据的点上没有小石头，那么 ta 就输了。请你找出所有的点 $v$，使得如果 crimson000 在游戏开始时把棋子放到 $v$ 上，他可以赢。
数据范围：$n\le 2000$。
如果我们当前在点 $u$，我们绝对不会走向一个 $a$ 值更大的点 $v$，因为如果我们走向 $v$，对方一定会选择走回来。如果我们再走向 $v$ 一定会把自己逼死。而我们走完这一趟还会让 $a_u$ 减少，更不利于我们接下来的行动。因此我们一定会选择走 $a_v< a_u$ 的点。
我们以每一个点为根跑 dp。我们设 $f_u$ 为在 $u$ 子树内走，先手是否必胜。转移我们就考虑 $u$ 的儿子中是否存在一个 $v$ 使得 $f_v=0$ 并且 $a_v<a_u$ 即可。
时间复杂度 $O(n^2)$，实现好点可以搞到 $O(n)$。
AGC011D
有 $n$ 个机器排成一排，有两种状态：$A$ 状态：会把球反弹（即让球反方向滚动）；$B$ 状态：让球自由通过（即让球沿原方向滚动）。
每有一个球撞上机器，这个机器就会改变状态 。
现在给你 $n$ 个机器的初始状态，然后你将一个球滚进去 $k$ 次，问 $k$ 次后所有机器的状态。
数据范围：$n\le 2\times 10^5, k\le 10^9$。
我们手玩样例可以发现：当滚过来一个球时，如果第一个机器为 $A$ 状态，那么它会直接弹回去，并且让开头的 $A$ 变成 $B$。如果开头是 $B$，那么这个球一定可以跑完所有的机器，并且我们可以发现规律：让所有机器的状态取反，并且再向左移位一格（第一个机器的状态跑到第 $n$ 个）。
我们找到这个规律之后就可以进行 $O(k)$ 的模拟了，因为常数小所以可以过。但是我们考虑再优化一下。
我们发现形如 ABABAB 这样的后缀是会保持不变，并且会不断往前扩展的。因为我们进行一次取反移位，最后这段会变为 BABABAX，而这个 X 是第一位过来的，因为进行一次循环移位必须第一位为 A，取反后变为 B 放到最后，这个后缀就扩展为了 BABABAB。每次循环移位会增加一位这个后缀，而每两个球放上去又至少会有一次循环移位，因此一定会在 $2n$ 次以内这个序列就会变为 ABABAB 或者 XABABAB。我们先暴力模拟 $2n$ 次，然后在看 $k$ 的奇偶性决定首位是什么。
时间复杂度 $O(n)$。
AGC011E
我们说一个数是“有影响力的”，当且仅当对于它的任意相邻的两位都有左边小于等于右边。
。
现在给你一个数 $n$，问最少可以被表示成几个有影响力的数之和。
数据范围：$1 ≤ n ≤ 10^{500000}$
我们考虑一个经典 trick：一个递增的数一定可以被表示成 $9$ 个形如 $11\cdots 11$ （包括 $0$）的数相加。我们设有 $t$ 个 $1$ 的 $11\cdots 11$ 为 $p_t$（$t\ge 0$）。那么 $n$ 就可以写成这样：
$$
n=\sum_{i=1}^{9k}p_{a_i}
$$
我们发现这样很难化简，但是我们发现 $p_t$ 用等比数列求和可以转化为 $\frac{10^{t}-1}{9}$。那么我们稍微化简下式子就能得到：
$$
9n+9k=\sum _{i=1}^{9k}10^{a_i}
$$
我们考虑在什么情况下这个等式是可以成立的。右边的式子如果没有任何进位的话，各个数位和应该是 $9k$，而当有进位时，一次进位就会让数位和减少 $9$，最终还是 $9$ 的倍数。因此我们要的就是要让 $9n+9k$ 的数位和不超过 $9k$，且为 $9$ 的倍数即可。
我们枚举 $k$，每次让 $n$ 加上 $9$，这样的复杂度是均摊 $O(1)$ 的。因此时间复杂度为 $O(n)$。
AGC012C
我们称一个字符串 $x$ 是好的当且仅当它满足以下条件：
- $x$ 可以被表示为另外一个串 $y$ 复制一遍得到，即 $x=\overline {yy}$。
- $x$ 非空。
现在要求一个串 $s$ 满足下列条件，可以证明这个串存在：
- $|s|\leqslant 200$
- 字符集大小为 $100$，每个字符用 $[1,100]$ 的整数表示。
- 在 $s$ 的所有的 $2^{|s|}$ 个子序列中，恰好有 $N$（$1 \le N \le 10 ^ {12}$）个串是好的，其中 $N$ 是给出的。
我们可以在前 $100$ 个数里先放一个 $1\sim 100$ 的递增序列，这样好串的数量就是 $[101, 200]$ 中的递增序列个数。
我们从 $1$ 到 $100$ 依次往里放，如果我们放到最右边，那么前面所有的上升序列后面都会放上它，好串数量变为二倍。而放到最左边，就只会增加它自己一个好串。
因此我们这个过程其实就类似于一个二进制拆分的过程。时间复杂度 $O(\log n)$。
AGC012D
$n$ 个球排成一排，第 $i$ 个球的颜色为 $c_i$，重量为 $w_i$。我们定义「一次操作」为：选择两个颜色相同，且重量之和不超过 $X$ 的球，交换它们的位置；或选择两个颜色不同，且重量之和不超过 $Y$ 的球，交换它们的位置。问进行任意次操作后，可以得到多少种不同的颜色序列。
数据范围：$n\le 2\times 10^5$。
我们将可以交换位置的球连边，手玩即可发现在一个连通块内的球是可以随便排列的。因此我们可以对每个连通块求一下多重集排列，最后相乘。时间复杂度 $O(n^2)$。
我们发现上面的做法复杂度太高的原因主要在于边数太多，可能达到 $O(n^2)$ 级别，但是我们只使用了连通性来求答案。因此我们考虑尽量缩减边数。
首先对于同色的两个球，我们考虑如果它们能够连边，那么也就意味着它们能和这个颜色的重量最小值连边。因此我们对于每种颜色，我们只让它们和该颜色的最小值连边即可。
而对于不同色的两个球，我们进行一个分讨。
我们先设 $a_c$ 为 $c$ 颜色里重量的最小值，我们再假设 $a_1\le a_2\le \cdots \le a_n$。我们考虑 $x$ 和 $y$ 这两种颜色的小球 $A$ 和 $B$，其中假设这两个小球是能够连边的，考虑什么时候这两个小球之间的边可以删去而不改变连通性。
- $x\not = 1, y\not = 1$，这时我们可以考虑让 $1$ 颜色的最小值直接和它们连边，连通性不会改变。
- $x\not =2, y\not =2$，这时我们可以让 $2$ 颜色的最小值和它们连边。
- $x=1, y=2$，这时会存在 $(x, a_2)$ 和 $(a_1, y)$ 两条边，同时一定有 $(a_1, a_2)$ 这条边。因此连通性不改变。
我们这里考虑到次小值的原因是：可能 $x$ 或 $y$ 为 $1$，又因为同种颜色限制不同而无法和最小值连边，可能会导致连通性改变。
我们用上面这三条规则即可连出一个边数只有 $O(n)$ 的图，时间复杂度 $O(n)$。
AGC013C
有一个长度为 $L$ 的圆环，上面有 $n$ 个蚂蚁，位置分别为 $x_i$，运动方向为顺时针或逆时针。每只蚂蚁将会同时开始以单位速度运动，如果两只蚂蚁相遇, 那么它们会改变自己的方向继续运动。求 $T$ 秒之后每只蚂蚁的位置。
数据范围：$n\le 10^5, L, T\le 10^9$。
我们先考虑序列上的这个问题。考虑一个经典 Trick：我们可以把蚂蚁相遇改变方向变为互相穿过，这样每个蚂蚁都互不影响了。而题目中给出的移动方式又可以得到蚂蚁的相对位置是不变的，因此我们只需要确定所有蚂蚁的位置后排序即可解决序列上的问题。
而对于环上的问题，我们只需要解决最终编号的问题。我们可以发现，编号的变化其实只和 $0$ 点有关。我们考虑一个蚂蚁如果逆时针越过了 $0$，那么它就到了序列的另一端，所有点的位置都会向左移动一位，而顺时针也同理。我们就可以计算一个蚂蚁越过了几次 $0$ 点，最终输出时错位一下即可。
时间复杂度 $O(n)$。
AGC013E
给定一个长度为 $n$ 的木板，木板上有 $m$ 个标记点，距离木板左端点的距离分别为 $X_i$，现在你需要在木板上放置一些不相交正方形，正方形需要满足
正方形的边长为整数
正方形底面需要紧贴木板
正方形不能超出木板，正方形要将所有的木板覆盖
标记点的位置不能是两个正方形的交界处
下面是一些满足条件与不满足条件的例子
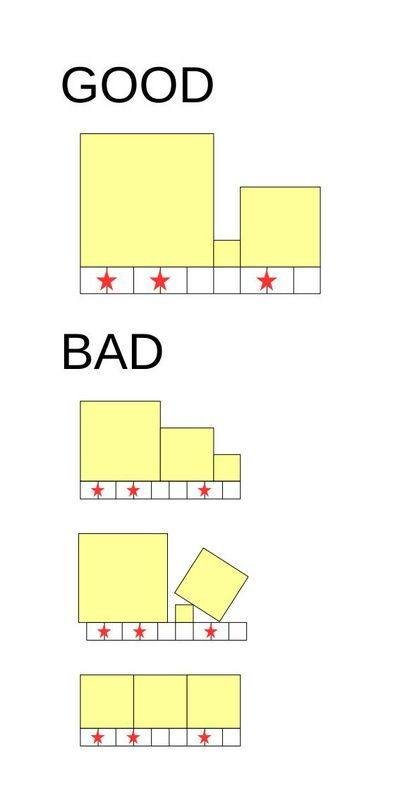
一种合法的正方形放置方案的贡献为所有正方形面积的乘积，也就是为 $\prod\limits_{i=1}^k a_i^2$，$a_i$ 为正方形的边长。请你求出所有合法方案的贡献之和。
数据范围：$n \leq 10^9$，$m \leq 10^5$。
牛逼题。
我们用组合意义把题目转化一下。我们现在要计算的其实是有 $n$ 个盒子，放置一些隔板，并且两个隔板之间的这些盒子中放两个互不相同的球（可放在同一个盒子）的方案数，其中有一些地方不能插板。这样就方便 dp 了。
我们设 $f_{i, j}$ 为第 $i$ 个盒子到它前面第一个隔板，这些盒子中放了 $j$ 个球的方案数。转移我们分情况讨论：
当是普通的空隙时，我们枚举当前放不放球以及放不放板可以得到下面的转移方程：
$$
f_{i, 0}=f_{i-1, 0}+f_{i-1, 2}
$$
$$
f_{i, 1}=2f_{i-1, 0}+f_{i-1, 1}+2f_{i-1, 2}
$$
$$
f_{i, 2}=f_{i-1, 0}+f_{i-1,1}+2f_{i-1,2}
$$
而是有限制的空隙时：
$$
f_{i, 0}=f_{i-1, 0}
$$
$$
f_{i,1}=2f_{i-1, 0}+f_{i-1,1}
$$
$$
f_{i,2}=f_{i-1,0}+f_{i-1,1}+f_{i-1,2}
$$
这时我们发现这个式子可以进行一个线性递推，矩阵快速幂即可。
时间复杂度 $O(m\log n\times 3^3)$。
AGC014D
给出一颗 $n$ 个节点组成的树，每个节点都可以被染成白色或者黑色。
有 crimson000（先手）和 Koishi（后手）两个人，crimson000 可以把任意一个点染成白色，Koishi 则可以把任意一个点染成黑色，每个点只可染色一次。
重复上述操作直到所有点都被染色后，只执行一次执行以下操作：
把所有 crimson000 染成黑色的节点的相邻的白点感染成“次黑色”。
次黑色不能继续感染白点。
若操作完毕后仍还有白点存在，即 crimson000（先手）胜，反之则 Koishi（后手）胜。
现在给出这棵树，问当前此树是先手必胜还是后手必胜。
数据范围：$n\le 10^5$。
手玩样例可以发现一个简单的事实：当一个点拥有两个作为叶子节点的儿子时，先手必胜，因为我们一定可以选择先放到这个节点，这时后手就会来不及顾及同时两个儿子。因此先手必胜。
而对于其他情况，我们这里给出结论：当一个点存在两个大小为奇数的子树时，先手必胜。我们可以按照这样的思路：我们先在一颗子树中选择一个最深的节点 $x$，我们就把 $x$ 的父亲染成白色。这时后手一定会选择染叶子。这样就类似于是把这两个点删去了，根据数学归纳法，最终会删成一个根节点加上这两个子树的根节点，这时这两个子树都删的只剩一个根节点，也就可以看成叶子了。这时情况就类似上面的情况了。
而对于不满足上面情况的情况，我们可以证明这时一定存在完美匹配。后手选择白点的匹配即可获胜。